関係がありそうで実は関係ない変数

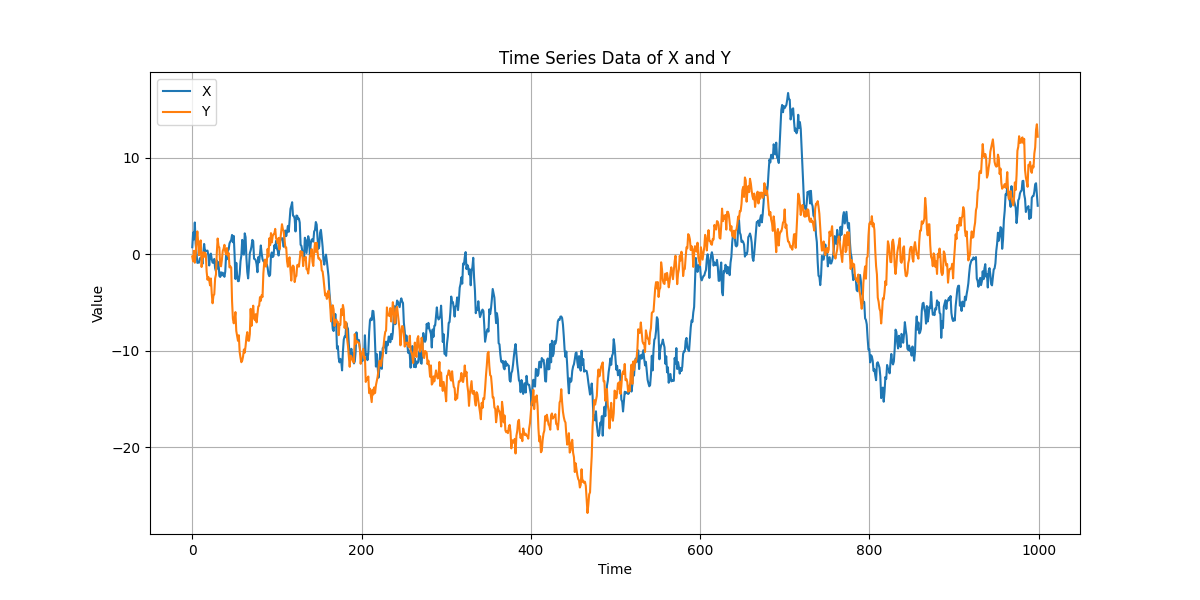
上のグラフはXとYの時系列推移をみたものです。両者は連動して動いているように見えます。

両者が連動しているという前提で、アナリストは両者の回帰分析を行ったり、比率をとってみたり、両者の差をとってみたりします。

種明かし：両者はランダム・ウォーク変数

実は、X、Yはそれぞれランダムに動いているだけです。
ランダム・ウォークする変数は文字通りランダムに動いているだけなので、XとYが連動しているように見えていても、実際には両者には何の連動性もありません。XとYは0を起点に、ホワイトノイズ（互いに無相関・同分散、平均ゼロ）を逐次1000個足していったものです。式で表現すると、

\(
X_t = X_{t-1} + \epsilon_t
\)

ここで、ϵtがホワイトノイズです。

偶然、連動しているような動きをしただけなので、今後ともそれらの動きが連動する必然性はありません。

両者の差をとってみると以下の図のような動きになります。

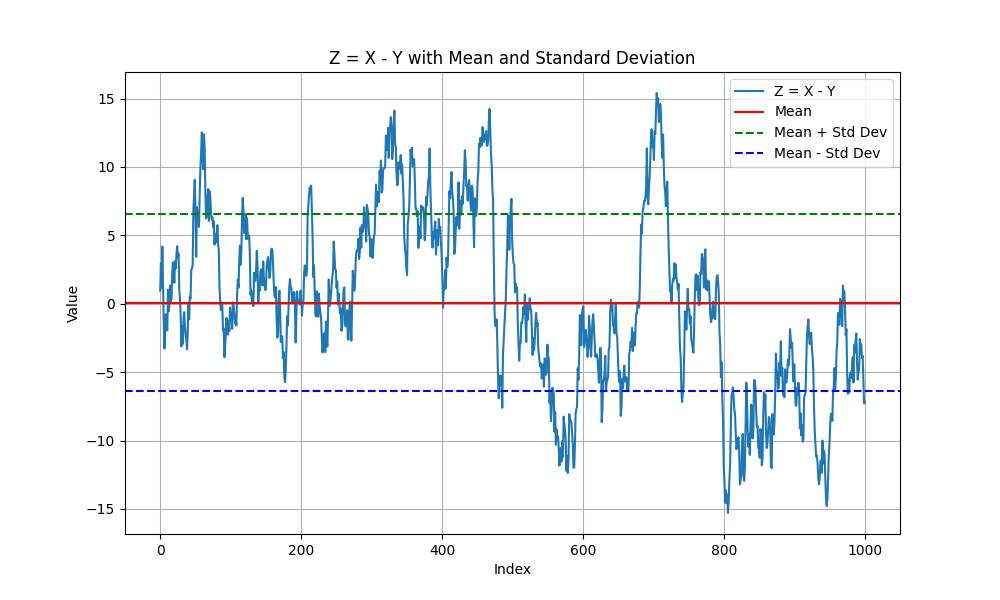
XとYの差（これをZとします）は一定の範囲内に収まるはずです。

実際、一定の幅（ここでは平均±1標準偏差）の中に多くのZが収まり、大きく乖離したときはゾーンの中に戻るような動きをしています。

しかし、繰り返しますが、もともと人工的にランダムに発生させた1000個のＸとＹが偶然に連動しているように見える動きをしただけなので、今後ともＺが一定の範囲内に戻る保証は全くないのです。

以上からわかる重要な示唆

ここではランダムに発生させた変数が偶然互いに連動しただけですが、ＸとＹの連動が経済理論的に保証されている場合には、両者は今後とも連動すると言えます。

したがって、過去のデータだけで判断するのではく、理論的な裏付けを基に、データでそれを検証することが重要です。

時系列分析での用語

ここで発生させたランダム変数は、単位根を持つ変数といいます。人工的にそのような変数を発生させたのですから、単位根をもっていて当然です。しかし、経済関係の時系列変数を扱う場合、単位根を持っているかどうか事前にはわかりませんので、まず「単位根検定」と呼ばれる検定を行います。

もし複数の時系列変数が単位根を持つことが検証された場合、次のステップとして、それらが連動しているかを検定します。これを「共和分検定」と言い、共和分関係を持つ場合は連動性を持っていることになります。

今回の記事で使用した二つのランダム変数は、単位根検定（ADF検定を使用）で単位根を持っているとの結果になりました。

また、共和分検定（Engle-Granger検定、Johansen検定を使用）でも共和分を持つとの結果になりました。

「見せかけの相関」が生じてはいても、共和分検定はパスしないことが多く、今回は珍しいケースになります。これが統計的仮説検定の限界ともいえますので、やはり重要なことは、過去のデータだけで判断するのではなく、理論的な裏付けがあるかどうかという点につきます。