10月22日の記事で資産取崩しのモンテカルロ・シミュレーションを行いましたが、平均収益率および収益率のバラつき(標準偏差)が一定であるとの前提を置けば、資産形成についても同様のシミュレーションを行うことができます。
再度確認しておくと、通常、株価はランダムウォークする確率変数で、この場合、株価平均値も株価のバラつきも一定ではなくなりますが、株式(投信)の収益率は一定の平均収益率周りを一定のバラつきを持って変動することが時系列分析の仮説検定で確認できます。収益率が平均値周りをどのようにバラつくかは確率的に変動するため、その実現値の推移は様々なパターンをとります。その様々なパターンを何通りもシミュレーションするのがモンテカルロ・シミュレーションで、ポトフォリオ・マネジメントや金融商品開発でよく使われている手法です。
ごく単純なモンテカルロ・シミュレーションを資産形成局面でやってみると、同じ条件設定にもかかわらず、将来の資産価値にかなり大きな違いが出る結果となりました。
平均収益率と標準偏差の初期設定について
9月30日の記事では、三菱UFJ eMAXIS Slim 米国株式(S&P500)の基準価額を使って2018年10月末から2024年9月27日まで積立シミュレーションしましたが、期間が短く、コロナ禍の暴落とその後の相場急回復の影響により、収益率がかなり高めに出ている可能性があります。そこで今回は、10月22日記事と同様、1994年から2024年までのS&P500TRの年あたり平均収益率10.63%と収益率の標準偏差22.68%を使うことにします。
シミュレーションの考え方
収益率は正規分布に従う確率変数であるとします。この場合、平均値周りで収益率がバラつくことになりますが、どのようにバラつくかは事前には予測できませんので、平均値以下の収益率が多頻度で実現した後、平均収益率を上回る収益率が多頻度で実現することもあるし、その逆も有りえます。収益率の実現パターンは無数にあり得るので、これを100通りシミュレーションし、積立投資累計額の将来の時価総額がどのような推移をたどるか見てみようというのが今回の目的です。
積立期間の設定
将来、雇用慣行が変わっていくでしょうが、現状では20代から働き初め、65歳定年が一般的と考えられますので、40年間毎月積立投資すると仮定します。現実には若い頃の積立額は小さく、ある程度年齢を経てから積立額を増額するのが一般的かもしれませんが、毎月の積立額はここでは1万円とします。これを40年間続けると、積立の累計額は480万円となります。NISA生涯投資枠は1800万円ですから、生涯で枠いっぱい使い切るなら、毎月3.75万円(1800/480)積み立てれば良いので、以下のシミュレーション結果も3.75倍して考えて下さい。
シミュレーション結果
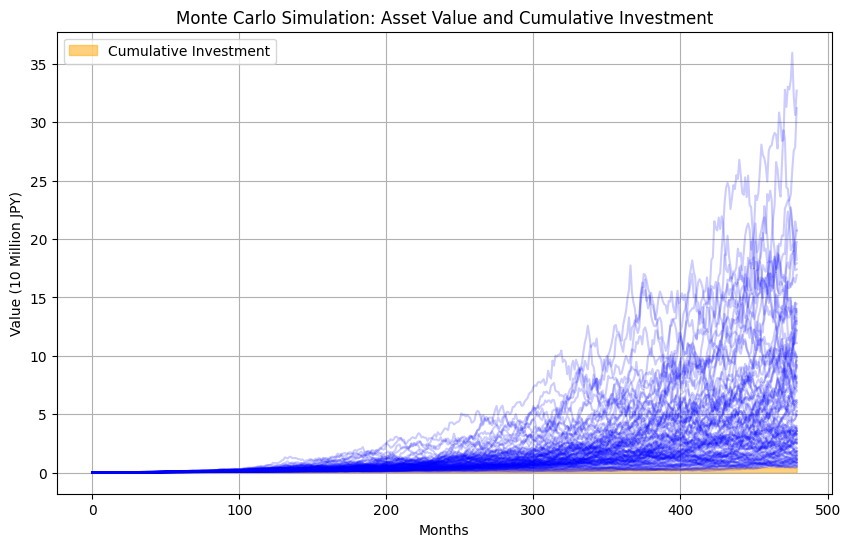
以上の前提でシミュレーションを100回行ってみました。シミュレーションの考え方としては、運用資産残高に毎月1万円追加投資し、年あたり平均収益率10.63%の月次換算値(10.63/12)が、年あたりの標準偏差22.68%の月次換算値(22.68/√12)でバラつくとし、これを各月の資産残高にかけて翌月の資産残高を逐次計算していくという方法です。そうして計算した100通りのシミュレーションが次のグラフです。
平均収益率と収益率の標準偏差の値をどのように設定するかで、シミュレーション結果は大きく違ってきますので、ここでのシミュレーションは一つの例に過ぎませんが、40年後の結果にこんなに大きな違いが出ることは、どのような方法でシミュレーションしても同じです。
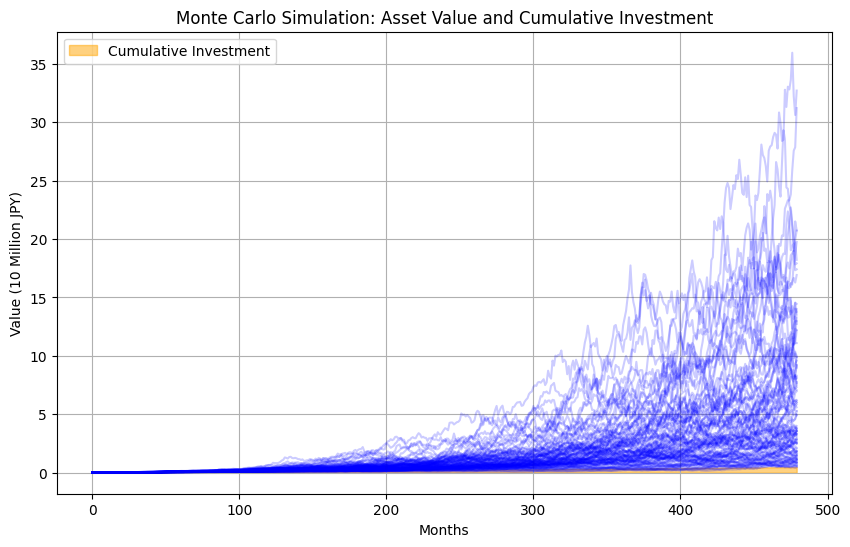
40年間の積立なので12ヶ月×40年=480ヶ月先まで100通りのシミュレーションを行っていますが、資産価値の推移を表す線が重なって見にくいので、480ヶ月後の100通りの結果のみを取り出すと以下のようになります。
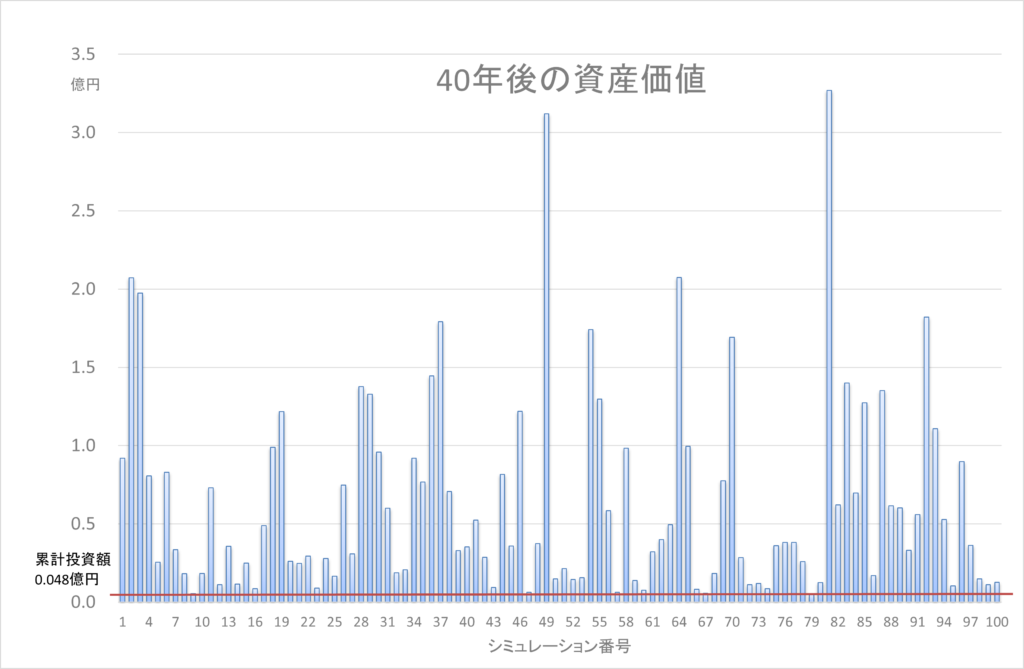
高い収益率が続いた場合、累計480万円の積立投資で、最高3億2690万円、最低470万円となりました。投資元本480万円を割り込んだのは、100回のシミュレーション中この1回のみで、ほか99回は480万円よりは大きくなってますので、よほど運が悪くない限り、40年間にわたって長期投資すれば元本割れの可能性は非常に小さいといえます。またかなり運が良ければ3億円を超える資産を形成できますが、全体の平均値としては6300万円の資産を形成できる結果になりました。
(注)以上の結果には注意点もあります。ここでは収益率が定常確率過程に従うことだけを前提にシミュレーションを行いましたが、株価指数(非定常確率過程)が他のマクロ経済変数(非定常確率過程)と共和分関係を保つ場合、その変数と株価指数の動きが連動することになります。例えば、EPS(一株利益)や名目GDPと株式時価総額が連動する場合、それらの動向から大幅に乖離して株価指数が動くことはないと言えます。
なおこれは累計投資額480万円のシミュレーション結果ですから、毎月3.75万円を40年間積み立ててNISA生涯投資枠1800万円を使い切った場合は、上記結果の3.75倍の資産を形成できることになります。もっとも、非常に小さい確率で元本割れもありうるので、運が悪ければ大きな資産は形成できない可能性もあります。
以上のプログラム
多数のシミュレーションをExcelを使って行うのは大変な労力なので、今回もPythonを使ってシミュレーションしました。参考までにプログラムを以下貼り付けます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# シミュレーションの設定
years = 40 # 積立期間(年)
months = years * 12 # 積立期間(月)
monthly_investment = 10000 # 毎月の積立額
annual_return = 0.1063 # 期待収益率(年率)
annual_volatility = 0.2268 # 収益率の標準偏差(年率)
simulations = 100 # シミュレーション回数
# モンテカルロシミュレーションの計算
np.random.seed(42) # 再現性のためにシードを固定
monthly_return = annual_return / 12 # 月次期待収益率
monthly_volatility = annual_volatility / np.sqrt(12) # 月次収益率の標準偏差
# 資産推移を格納するリスト
asset_values = np.zeros((simulations, months))
cumulative_investment = np.arange(1, months+1) * monthly_investment
# 各シミュレーションを実行
for i in range(simulations):
portfolio_value = 0
for month in range(months):
# 毎月の積立
portfolio_value += monthly_investment
# ランダムなリターンを生成
random_return = np.random.normal(monthly_return, monthly_volatility)
# ポートフォリオ価値にリターンを適用
portfolio_value *= (1 + random_return)
asset_values[i, month] = portfolio_value
# 各シミュレーションの最終資産価値と積立累計額をデータフレームにまとめる
simulation_data = pd.DataFrame(asset_values.T, columns=[f'Simulation {i+1}' for i in range(simulations)])
simulation_data['Cumulative Investment'] = cumulative_investment
# グラフを描画
plt.figure(figsize=(10, 6))
# 複数のシミュレーションの資産推移
for i in range(simulations):
plt.plot(asset_values[i] / 1e7, color='blue', alpha=0.2) # 縦軸を1000万円単位に
# 積立累計額を表示(面グラフ)
plt.fill_between(range(months), cumulative_investment / 1e7, label='Cumulative Investment', color='orange', alpha=0.5)
# グラフの設定
plt.title('Monte Carlo Simulation: Asset Value and Cumulative Investment')
plt.xlabel('Months')
plt.ylabel('Value (10 Million JPY)') # 縦軸は1000万円単位
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()