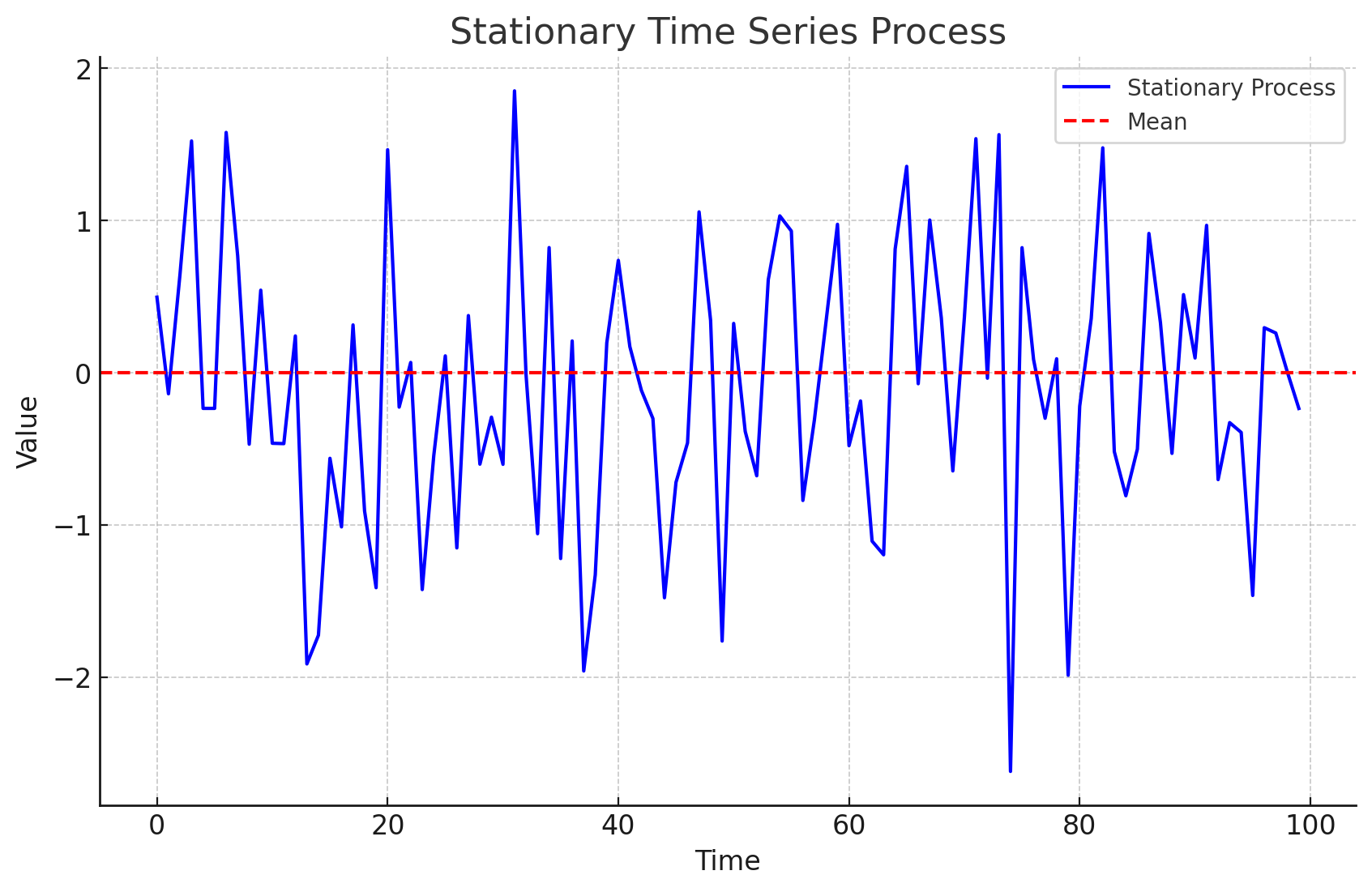
S&P500とTOPIXの収益率が持つ性質; 時系列分析で見える共通点

10月6日記事で行ったS&P500連動投信を取り崩すシミュレーションでは、投資収益率が平均回帰の性質のため一定の範囲に収まることを、暗黙に想定していました。

統計的にこのことを確認してから、次回はTOPIXについても同様のシミュレーションを行うことにします。

定常確率過程と非定常確率過程
取崩しシミュレーションで前提としていたこと
S&P500とTOPIXの収益率は？
まとめ

定常確率過程と非定常確率過程

時系列データには、定常確率過程と非定常確率過程とがあり、金融時系列データの多くは非定常であることがわかっています。

非定常性と定常性の違いは、確率過程におけるデータの時間的な性質や挙動に関するものです。

1. 定常性（Stationarity）

定常性を持つ確率過程では、データが時間に依存せず、一定のパターンを持ちます。これには強定常性と弱定常性とがありますが、一般に「定常性」と言えば弱定常性を指します。

定常データは次の3つの条件を満たします：

平均が一定：データの平均値が時間に依存せず変わらない。
分散が一定：データの散らばり具合が一定。
自己共分散が時間差に依存する：データの自己共分散がラグ（時間差）にのみ依存し、時間そのものには依存しない。

これらの条件が満たされている場合、データは時間が経過しても安定的な動きを示します。長期的なトレンドや季節性がないため、多くの時系列モデルがこの定常性を前提としています。

定常性の特徴：

データが時間の経過に対して安定している。
長期的なトレンドや季節的な影響はなく、データが一定範囲内で振動する。
分析や予測がしやすい（多くの時系列モデルが定常性を前提とする）。

イメージとして、定常確率過程に従うデータは次のような挙動をします。

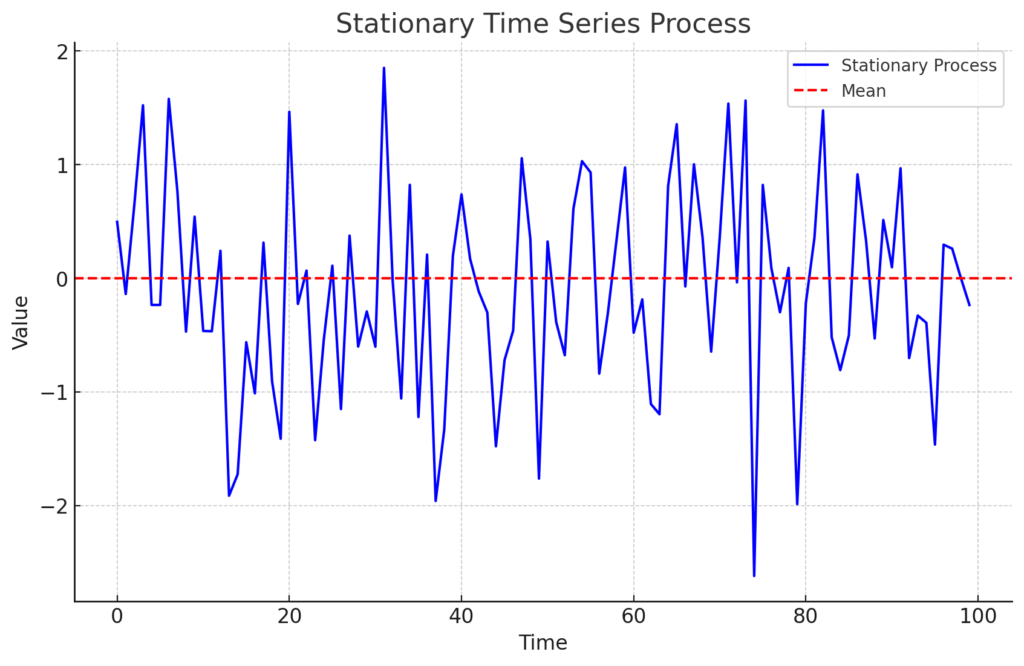
2. 非定常性（Non-stationarity）

非定常性を持つ確率過程では、データの性質が時間とともに変化します。これにより、平均や分散、自己共分散が時間に依存するため、次のような特徴を示します：

平均が変動：時間が進むにつれてデータの平均値が変わっていく（例：上昇トレンドや下降トレンドがある）。
分散が変動：データの散らばり方（分散）が時間とともに変わる。
自己共分散が不安定：異なる時点のデータ間の関係が、時間差だけでなく、時間そのものに依存してしまう。

非定常性の特徴：

長期的なトレンド（上昇や下降）や季節性が見られることが多い。
分析や予測が困難になることが多い。
一般的には、データを差分化（差分や変化率を取る）やトレンド除去によって定常化する必要がある。

取崩しシミュレーションで前提としていたこと

資産の収益率がもし非定常確率過程に従いランダムに変動するなら、収益率が平均回帰せず一方方向へ変化し続けることもありえます。資産の増加率（収益率）と取崩し率が等しければ、資産を減らすことなく運用収益をキャッシュアウトできるのが定率取り崩しの利点ですが、収益率が一方方向に変動してしまうと、取崩し率との乖離が拡大し続ける可能性があります。

取崩し率＞収益率の乖離が拡大する場合、資産が減り続けるし、取崩し率＜収益率の乖離が拡大する場合、資産が増え続け、資産寿命が不安定化してしまうため、定率取り崩しの考え方が意味のないものになってしまいます。

他方、収益率が一定の平均値（＝定率取崩し率）に沿って変動するのであれば、平均値から乖離した場合、やがて平均値へ回帰することになります。この場合は、定率取崩しが意味のあるものになり、収益率が下振れして取崩し額が小さくなると、その後、収益率が上振れもして（結果的に平均値が一定の値となる）、取崩し額が大きくなる局面も出てきます。10月6日記事でS&P500を使ってシミュレーションした際には確かにそのようになっていました。

S&P500とTOPIXの収益率は？

配当を再投資した場合のS&P500トータルリターンインデックスに相当するものとして、TOPIX配当込み指数があります。

S&P500トータルリターンインデックス、TOPIX配当込み指数ともに、その収益率が定常か非定常かを検証するADF検定結果は次のようになりました。

期間（1991-2024年）	TOPIX収益率	S&P500収益率
ADF検定量	-5.951	-5.877
p値	0.000	0.000
使用ラグ数	0	0
観測数	34	34
1%臨界値	-3.639	-3.639
5%臨界値	-2.951	-2.951
10%臨界値	-2.614	-2.614