資産取崩しのモンテカルロ・シミュレーション

10月6日記事では、S&P500トータルリターンインデックス（円建て、以下S&P500TR）の実績値を使い、30年前の1994年にS&P500連動投信を1000万円分保有していたとして、毎年初に定率10％で取崩しながら残りを30年間運用するシミュレーションを行った結果、2024年初に運用資産が1246万円となりました。ただしこの結果は、収益率が確率変数である以上、無数にあり得るパターンでの一つの結果に過ぎません。

10月8日記事で、S&P500TRの収益率が一定の平均値とバラツキ（標準偏差）を持つことを確認しました。S&P500TRの1994年初から2024年初までの累積収益率の年あたり収益率は10.63％、収益率（資産額の前年比）の標準偏差は22.68％だったので、今後も同じ平均収益率、標準偏差を持つという前提で、運用資産の推移をモンテカルロ・シミュレーションしてみました。

（注）モンテカルロ・シミュレーションでは、無数のシナリオを生成して、異なる将来をシミュレートします。これにより、将来の結果の不確実性やリスクの範囲を評価できる点は非常に有効です。ただし、経済環境や市場の構造が変わる場合、過去のデータに基づいたシミュレーション結果が実際の未来を反映しない可能性はあります。

定額取崩し

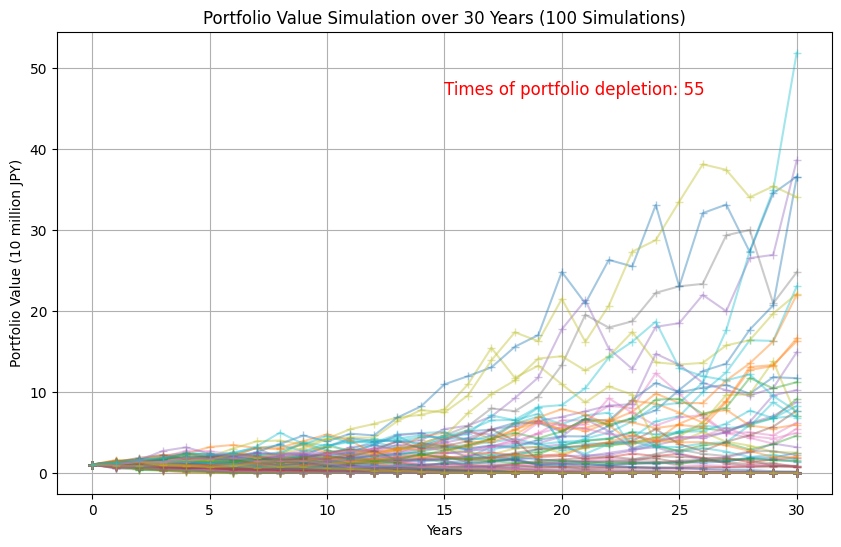
初期額を1000万円として、その10％に相当する金額100万円を30年間、毎年初に定額取崩すシミュレーションを100回行ってみたところ55回、途中で資産が枯渇しました。反面、高い収益率が最も多く実現したときは、30年後の資産残高が5億円を超えました。他方、定額取崩し額を50万円とすると、100回のうち15回、途中で資産が枯渇しました。

定額取崩しのPythonプログラム

シミュレーションに使用したPythonプログラムは以下のようになります。赤字部分は、定率取崩しにする場合に必要な変更箇所です。

import numpy as np
import matplotlib.pyplot as plt

# 初期設定
initial_investment = 10000000  # 初期投資額 1000万円
rate_of_return = 0.1063  # 収益率 10.63%
std_deviation = 0.2268 # 収益率の標準偏差 22.68%
withdrawal_rate = 0.10  # 取り崩し率 10%
years = 30  # シミュレーション年数
simulations = 100  # シミュレーション回数

# 再現性確保のためrandom.seedを1に指定
np.random.seed(1)
depletion_count = 0  # 資金枯渇回数のリセット

# 取り崩し額（定額）
withdrawal_amount = initial_investment * withdrawal_rate

# 複数回のシミュレーションを実行
portfolio_simulations = []
for sim in range(simulations):
    portfolio_values = [initial_investment]
    for year in range(1, years + 1):
        annual_return = np.random.normal(rate_of_return, std_deviation)
        portfolio_value = portfolio_values[-1] * (1 + annual_return)
        portfolio_value_after_withdrawal = portfolio_value - withdrawal_amount
        portfolio_value_after_withdrawal = max(portfolio_value_after_withdrawal, 0)
        portfolio_values.append(portfolio_value_after_withdrawal)

    # 最終年で資産が0になっていた場合、資産枯渇とみなす
    if portfolio_values[-1] == 0:
        depletion_count += 1

    portfolio_simulations.append(portfolio_values)

# グラフ描画
plt.figure(figsize=(10, 6))
for sim in portfolio_simulations:
    plt.plot(range(0, years + 1), [val / 1e7 for val in sim], marker='+', linestyle='-', alpha=0.4)

plt.title('Portfolio Value Simulation over 30 Years (100 Simulations)')
plt.xlabel('Years')
plt.ylabel('Portfolio Value (10 million JPY)')  # 単位1000万円
plt.grid(True)

# 資産枯渇回数をグラフの中に追加
plt.text(15, max([max(sim) for sim in portfolio_simulations]) / 1e7 * 0.9,
         f"Times of portfolio depletion: {depletion_count}", fontsize=12, color='red')

plt.show()

定率取崩し

毎年初に資産の10％相当額を取崩す場合、資産が減れば取崩し額も減るため資産が枯渇することはありません。30年間定率取崩し・運用しても、運が良ければ約2700万円の資産が残り、悪くても約200万円残る結果になりました。

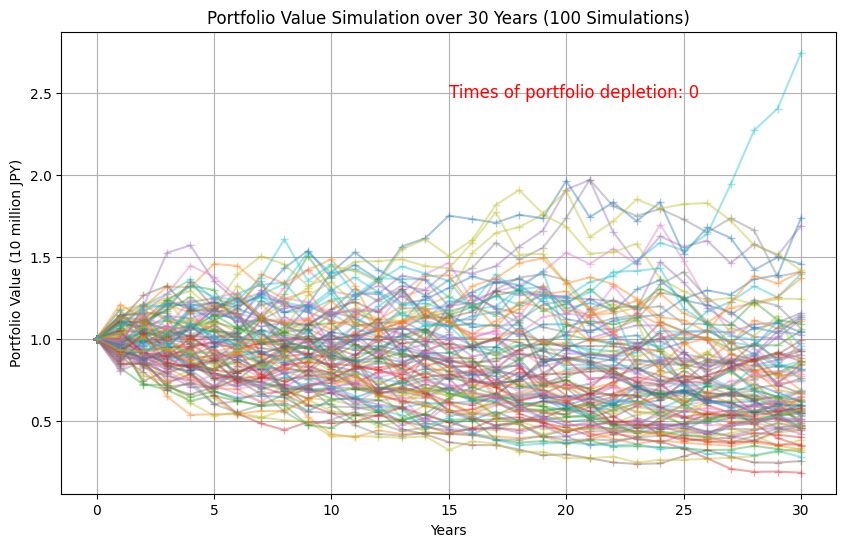
取崩し率が平均収益率よりも高ければ、資産は枯渇しないとしても、増えることはなく減っていくはずです。20％定率取崩しするケースでシミュレーションすると、時間の経過とともに資産が減少していきます。

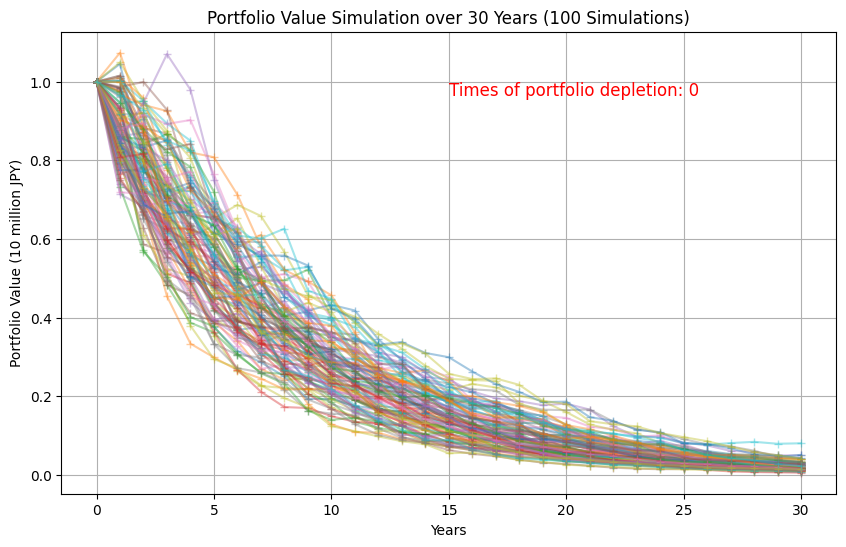
逆に、平均収益率よりも低い率である5％で定率取崩しとすると、時間の経過とともに資産が増えていくケースがほとんどで、運用期間中、減少し続けることはありませんでした。

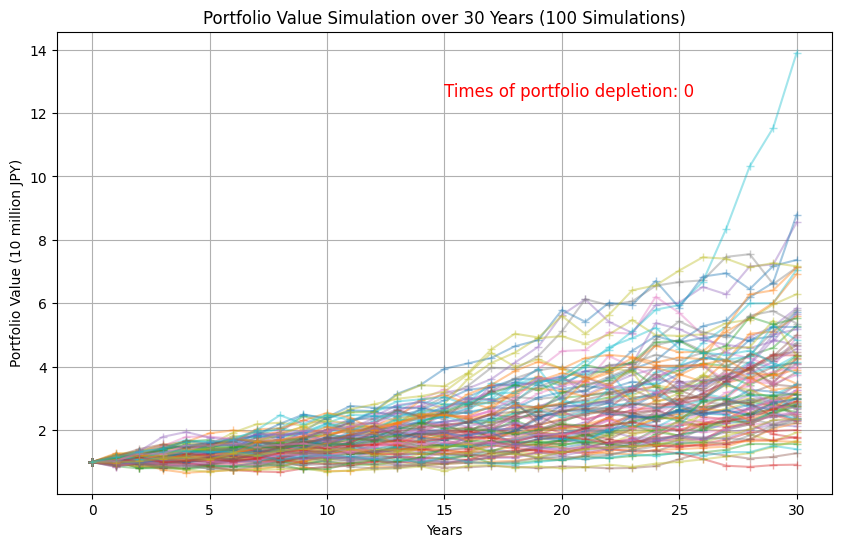
コードの変更箇所

定額取崩しのコード

# 取り崩し額（定額）
withdrawal_amount = initial_investment * withdrawal_rate

部分を削除し、

portfolio_value_after_withdrawal = portfolio_value - withdrawal_amount

部分を

portfolio_value_after_withdrawal = portfolio_value * (1 - withdrawal_rate)

と書き換えると、定率取崩しになります。資産枯渇は起こらないので他にも不要なコードがありますが、そのままでも結果に影響はありません。

まとめ

毎年の収益率が確率変数なので、30年間の取崩し・運用では無数のパターンが有りえます。そこでモンテカルロ・シミュレーションを行うと、

• 定額取崩しの場合、運用期間中に資産が枯渇する可能性がある一方、資産が初期額より大幅に増える可能性もある。
• 定率取崩しの場合、資産枯渇リスクはないものの、平均収益率よりも取崩し率を高く設定すると、取崩し額が減少していく可能性がある。
  • ただし、年齢を重ねると必要な生活費が減少していくと考えるなら、平均収益率並かそれ以上の定率取崩し率とする考え方は有りえる。
• 平均収益率よりも低い定率取崩し率の場合、運用期間を通じ資産が増加していくが、個人が形成した資産を生涯で使い切るという考え方ではなくなり、年金基金や公益法人などのエンダウメント運用で活かされる考え方になる。